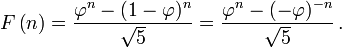|
The ratio between two numbers is the result of dividing one number by the other.
For example, the ratio between 12 and 3 is 4, while the ratio between 1 and 2 is 0.5.
Consider the problem of dividing a segment in two segments (one large and one small) such that the ratio between the large segment and the whole is equal to the ratio between the small segment and the large segment.

|
|
This problem was known to the ancient Greeks who called this ratio golden.
Nowadays this ratio is commonly called phi, which is the Greek letter for F. The Greek sign for this letter is ɸ (or φ, in lowercase). This letter was chosen to honor Leonardo Fibonacci.
After solving a simple quadratic equation, the numeric value of phi can be determined to be:
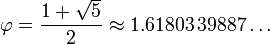
A golden rectangle is a rectangle whose width divided by its height yields Phi.
Strangely enough, we humans perceive shapes as proportioned when they can be enclosed in a golden rectangle. The ancients knew this. Thus, for example, the Greek Parthenon can be repeatedly enclosed in a golden rectangle as illustrated below:

The golden ratio is also called the divine proportion because it is closely related to how we perceive things as beautiful and proportioned.

Phi can be approximated by dividing two consecutive Fibonacci numbers:
| Term | Previous | Ratio |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 2 | 1.5 |
| 5 | 3 | 1.6666 |
| 8 | 5 | 1.6 |
| 13 | 8 | 1.625 |
| 21 | 13 | 1.6153 |
| 34 | 21 | 1.619 |
| 55 | 34 | 1.6959 |
| 89 | 55 | 1.6181 |
| 144 | 89 | 1.6179 |
| 233 | 144 | 1.6180 |
As we can see, when we divide consecutive Fibonacci numbers their ratio quickly approaches 1.61803399. This value is none other than Phi!
On a curious note, Phi itself can be used to compute any term of the Fibonacci series by applying the formula below: