The Fibonacci Numbers in Nature

At this point you may wonder what the Fibonacci series has to do with real life. Well, for one, the number of petals in a flower is usually a Fibonacci number.

As you may recall, the Fibonacci series is 0, 1, 1, 2, 3, 5, 8 and so on. Consider the flowers presented below:

	This flower is called a pink trillium. It has 3 petals, which is the 5th term of the Fibonacci series.
	This flower is called a larkspur. It has 5 petals, which is the 6th term of the Fibonacci series.
	This flower is called a pink clematis. It has 8 petals, which is the 7th term of the Fibonacci series.

For more information on this subject, please go to my page on flowers.

The Fibonacci series can be applied to animals as well.

Let us say that we have one pair of rabbits, one male and one female. These rabbits reproduce according to the following rules:

• No pair of rabbits dies
• Rabbits always have 2 babies per pair and each pair is always one male and one female
• Each pair mates and has another pair two months after birth and then has a pair every one month

We will start on month 1 here representing first term.

The first month we start with 1 pair. The second month we still have 1 pair because it has not reproduced yet. The next month there are 2 pairs because the first pair has reproduced once The next month there are 3 pairs because the first pair reproduces again The next month there are 5 pairs because the second pair starts to reproduce and because the first pair has reproduced again The next month... well, you get the point

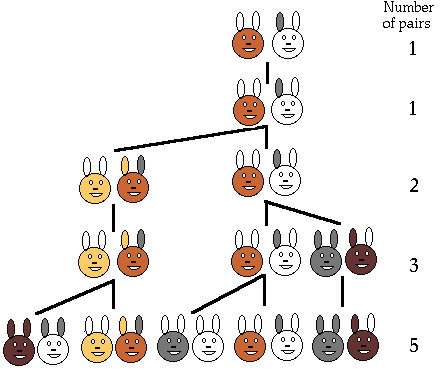
Let us see another similar example.

Dudeney's Cows

Henry E. Dudeney was an English puzzlist who lived between 1857 and 1930. He wrote many interesting books including 536 Puzzles and Curious Problems. On his 175th problem he wrote another way of relating the Fibonacci numbers to nature.

Suppose that there is one female cow and an unlimited amount of males to breed with. Like in the rabbit problem above,

• every cow can mate 2 years after birth and then every one year
• the only babies born are females

According to these rules:

• First year: One newborn female calf
• Second year: One female cow almost ready to breed
• Third year: 2 female cows
• Fourth year: 3 female cows
• Fifth year: 5 female cows
• Sixth year: 8 female cows