
|
A series is just a collection of numbers following a pattern.
For instance, the series of natural numbers is:
In the above series we start with the number 1. The pattern is simple: we add one to the previous number.
We refer to each number in a series as a term. For instance, 4 and 5 five are two consecutive terms of the natural number series.
Let's look at another series:
Here, the initial number is 4. The rule is doubling the previous number.
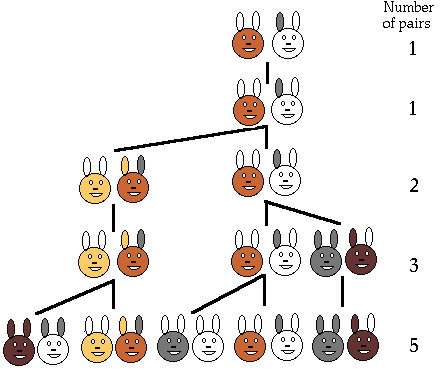
The Fibonacci series has two initial numbers: 0 and 1. The rule is to add the two previous numbers together:
The following image provides a visual representation of the Fibonacci series:

Here, the length of each line is the sum of the lengths of the two previous lines.
You may be wondering: How does this relate to the real world?. Well, if we turn these lines clockwise and place them next to a human body, look at what we get:

Yes: we perceive people as normal as long as their bodies meet these proportions!
For instance, in the arm below, if we divide the length of the hand by the length of the forearm we get a value that is very close to that of dividing two consecutive terms of the Fibonnaci series.

The Fibonacci numbers occur in nature very frequently, like in flowers and, indeed, in many living organisms.
When we divide two consecutive numbers of the Fibonacci series, the result approaches a special value called the Golden Ratio.